本文介绍数据结构课程中,经典的排序算法:冒泡、选择、插入、快速排序、希尔排序、归并排序、堆排序等…算法中的代码使用java语言实现。
冒泡排序
1、算法:
- 设想被排序的数组R[0..N]垂直竖立,从下往上扫描数组R,依次相邻两两比较元素,将小数放在前面,大数放在后面;
- 这样,一次比较之后,最小的元素就被交换到了第一个位置;
- 如此反复,继续从下往上扫描,知道最后两个元素。
2、实现:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15static void maopao() {
for (int i=0;i<a.length-1;i++) {
for (int j=a.length-1;j>i;j--) {//从下到上依次两两比较,把较小的排到前面
if (a[j] > a[j-1]) {
int tmp = a[j];
a[j] = a[j-1];
a[j-1] = tmp;
}
}
}
System.out.println("------排序结果----------");
for (int ai:a) {
System.out.println(ai);
}
}
3、时间复杂度:
冒泡排序总的平均时间复杂度为:O(n2);冒泡排序是稳定的排序算法;
4、优化:
- 某一趟遍历如果没有数据交换(内存循环),则说明已经排好序了,因此不用再进行迭代了。用一个标记记录这个状态即可。
- 在第一步优化的基础上发进一步思考:假设R[0..i]已是有序区间,上次的扫描区间是R[i..n],记上次扫描时最后一次执行交换的位置为lastSwapPos,则lastSwapPos在i与n之间,不难发现R[i..lastSwapPos]区间也是有序的,否则这个区间也会发生交换;所以下次扫描区间就可以由R[i..n] 缩减到[lastSwapPos..n]。
优化后的代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22static void maopao1() {
int lastPos = 0,lastPosTmp = 0;
for (int i=0;i<a.length-1;i++) {
lastPos = lastPosTmp;
for (int j=a.length-1;j>lastPos;j--) {
if (a[j] > a[j-1]) {//把最小的元素选出来
int tmp = a[j];
a[j] = a[j-1];
a[j-1] = tmp;
lastPosTmp = j;
}
}
if (lastPos == lastPosTmp) {
break;
}
}
System.out.println("------排序结果----------");
for (int ai:a) {
System.out.println(ai);
}
}
补充:排序的稳定性是指排序后数列中的相同数的相对位置没有改变 ;不稳定性排序则改变了相同数的相对位置。
选择排序
1、算法:
- 从第一个元素开始(作为标杆),依次和后面元素比较,按照从大到小/从小到大交换位置;
- 这样,一次比较之后,最大/最小的元素就被交换到了第一个位置;
- 接下来,对第二个元素进行同样的操作,直到最后一个元素。
2、代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15static void xuanze() {
for (int i=0;i<a.length-1;i++) {
for (int j=i+1;j<a.length;j++) {
if (a[i] > a[j]) {//把最小的元素选出来,放到第一个位置
int tmp = a[i];
a[i] = a[j];
a[j] = tmp;
}
}
}
System.out.println("------排序结果----------");
for (int ai:a) {
System.out.println(ai);
}
}
3、时间复杂度:
时间复杂度都为O(n2),而且它还需交换元素(n-1)次和移动元素3(n-1)次;它是不稳定的排序算法。
插入排序
1、算法:
- 将初始序列中的第一个元素作为一个有序序列;
- 将剩下的 n-1 个元素按关键字大小依次插入该有序序列中;
- 每插入一个元素后依然保持该序列有序,经过 n-1 趟排序后使初始序列有序。
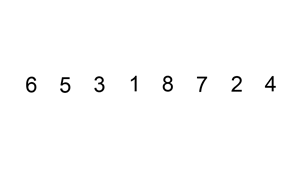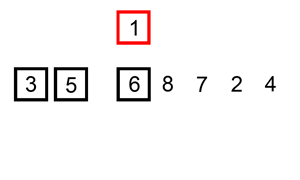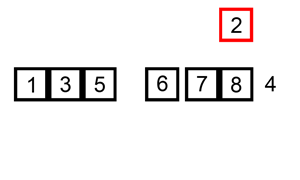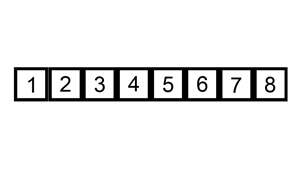
注:插入排序分为直接插入、折半插入,这里只介绍直接插入。
2、代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15static void charu() {
for (int i=1;i<a.length;i++) {
int tmp = a[i];
int j = i;
while (j>0 && a[j-1]>tmp) {
a[j] = a[j-1];
j -- ;
}
a[j] = tmp;//插入
}
System.out.println("------排序结果----------");
for (int ai:a) {
System.out.println(ai);
}
}
3、时间复杂度:
时间复杂度为O(n2);插入排序是稳定的排序算法。
快速排序
1、算法:
- 从数列中挑出一个元素作为基准数。
- 分区过程,将比基准数大的放到右边,小于或等于它的数都放到左边。
- 再对左右区间递归执行第二步,直至各区间只有一个数。
快速排序采用的思想是分治思想。他之所比较快,因为相比冒泡排序,每次交换是跳跃式的。
2、代码:(递归、关键点在于获取中轴)1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34static void kuaipai() {
int left = 0,right = a.length-1;
quickSort(a,left,right);
System.out.println("------排序结果----------");
for (int ai:a) {
System.out.println(ai);
}
}
private static void quickSort(Integer[] data,int left,int right) {
if (left < right) {//递归推出
int p = partition(a,left,right);//获取中轴
quickSort(a,left,p-1);//递归计算左边
quickSort(a,p+1,right);//递归计算右边
}
}
//获取中轴
private static int partition(Integer[] data,int left,int right) {
int tmp = data[left];//以第一个元素作为中轴
while (left < right) {
while (left < right && data[right] >= tmp) {
right --;
}
data[left] = data[right];//比中轴小的记录移到低端
while (left < right && data[left] <= tmp) {
left ++;
}
data[right] = data[left];//比中轴大的记录移到高端
}
data[left] = tmp; //中轴记录到尾
return left; //返回中轴的位置
}
3、时间复杂度:
平均时间复杂度为O(NlogN),最坏情况也为O(n2)
希尔排序
1、算法:
- 把记录按步长 gap 分组,对每组记录采用直接插入排序方法进行排序(步长相等的元素为一组)
- 随着步长逐渐减小,所分成的组包含的记录越来越多,当步长的值减小到 1 时,整个数据合成为一组,构成一组有序记录,则完成排序。
希尔排序属于插入类排序增强版,是将整个无序数组,按照某个步长gap分割成若干小的子序列分别进行插入排序,然后再减小步长。其思想采用分治思想,通过对较小的序列进行插入排序,然后对基本有序的数列进行插入排序,能够提高插入排序算法的效率。
2、代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22static void shellSort() {
int gap = a.length/2;
while (0<gap) {
for (int i=gap;i<a.length;i++) {//一个完整的插入排序,只是步长为gap不再是1 了
int j = i;
int tmp = a[i];
while (j-gap>=0 && a[j-gap]>tmp) {
a[j] = a[j-gap];
j = j-gap;
}
a[j] = tmp;
}
gap = gap/2;//缩小步长
}
System.out.println("------排序结果----------");
for (int ai:a) {
System.out.println(ai);
}
}
3、时间复杂度:
平均时间复杂度为O(NlogN);不稳定
归并排序
1、算法:
- 把 n 个记录看成 n 个长度为 l 的有序子表
- 进行两两归并使记录关键字有序,得到 n/2 个长度为 2 的有序子表
- 重复第 2 步直到所有记录归并成一个长度为 n 的有序表为止
归并排序,指的是将两个已经排序的序列合并成一个序列的操作(即把待排序的序列分成若干个子序列,每个子序列都是有序的,然后把有序子序列合并成整体有序序列)。归并排序有多路归并排序、两路归并排序 , 可用于内排序,也可以用于外排序。这里仅对内排序的两路归并方法进行讨论。该算法也是采用了分治思想。
2、代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45static void guibing () {
gbSort(a,0,a.length-1);
System.out.println("------排序结果----------");
for (int ai:a) {
System.out.println(ai);
}
}
private static void gbSort(Integer[] data,int low,int hight) {
int mid = (low+hight)/2;
if (low < hight) {//递归退出条件
gbSort(a,low,mid);//左边有序
gbSort(a,mid+1,hight);//右边有序
merge(a,low,mid,hight);//将左右两边有序的数组合并
}
}
private static void merge(Integer[] data,int low,int mid,int hight) {//将有二个有序子数组a[begin...mid]和a[mid+1...end]合并。
int[] temp = new int[hight - low + 1];
int i = low;// 左指针
int j = mid + 1;// 右指针
int k = 0;
// 把较小的数先移到新数组中
while (i <= mid && j <= hight) {
if (data[i] < data[j]) {
temp[k++] = data[i++];
} else {
temp[k++] = data[j++];
}
}
// 把左边剩余的数移入数组
while (i <= mid) {
temp[k++] = data[i++];
}
// 把右边边剩余的数移入数组
while (j <= hight) {
temp[k++] = data[j++];
}
// 把新数组中的数覆盖nums数组
for (int k2 = 0; k2 < temp.length; k2++) {
data[k2 + low] = temp[k2];
}
}
3、时间复杂度:
归并排序的最好、最坏和平均时间复杂度都是O(nlogn),而空间复杂度是O(n);归并排序算法比较占用内存,是稳定的排序算法。